CI Motor Montajlarının Yorulma Analizi için Yeni Bir Yaklaşım
Endurica Çözümlerinin Temel Fikri
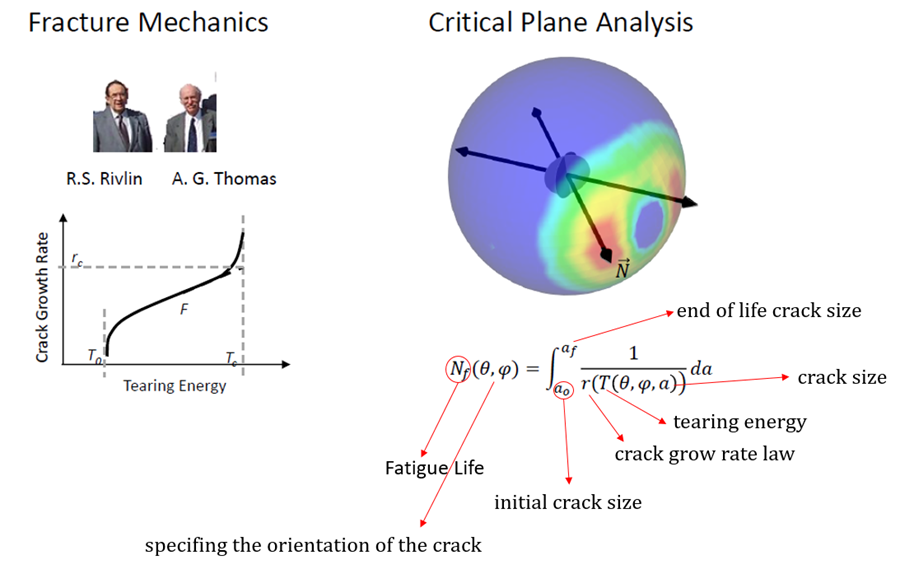
Şekil 1’de gösterilen Kırılma mekaniği, kauçukların analiz edilmesi ve test edilmesi için kullanılan bir yaklaşımdır ve ilk olarak Rivlin ve Thomas tarafından geliştirilmiştir. Temel fikir, bir malzemenin dayanımının, bir çatlağın büyüyüp büyümeyeceğinin ve büyüme hızının, yırtılma enerjisi (enerji yayılım hızı) kullanılarak karakterize edilebileceğidir.
- X ekseninde, yırtılma enerjisi çatlağa uygulanan yükün şiddetini yansıtır. Yük arttıkça, çatlak daha hızlı büyür.
- Kırılma mekaniğindeki güçlü bir kavram, çatlak büyümesinin yırtılma enerjisi cinsinden karakterize edilmesi durumunda, çatlağın şeklinin önemsiz hale gelmesidir. Tüm ayrıntılar, çatlak büyüme hızını yırtılma enerjisine bağlayan tek bir temel eğride birleşir.
Yorulma Ömrü Tahmini
Bu yaklaşım, hem deneysel hem de analitik olarak önemli avantajlar sunar. Yorulma ömrünü tahmin etmek için bir integral hesaplarız:
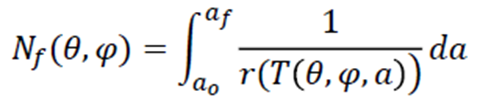
Çatlak Yönelimi ve Kritik Düzlem Analizi
- Yorulma ömrü , çatlağın yönelimini tanımlayan θ ve φ açılarına bağlıdır.
- Oklar, bir çatlağın düzlemine tanımlayan normal vektörleri temsil eder.
- Her normal vektörle ilişkilendirilmiş, küçük ve madeni para(gibi) şeklinde bir çatlak düzlemi bulunmaktadır.
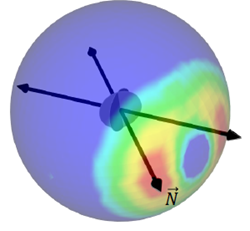
Kritik düzlem analizinde, tüm olası çatlak yönelimlerini (her yöndeki vektörleri) değerlendiririz. Her düzlem için, yorulma ömrünü hesaplamak üzere integrali çözeriz
Bir küresel alan üzerinde kontur grafiği olarak çizildiğinde, yorulma ömrü dağılımı görselleştirilir.
- Mavi bölgeler uzun ömrü gösterir.
- Kırmızı bölgeler kısa ömrü gösterir.
Amaç, en koyu kırmızı rengi üreten çatlak yönelimini belirlemektir; bu, minimum ömür tahminini temsil eder. Bu yönelim, çatlak büyümesi için en kritik düzlemi vurgular.
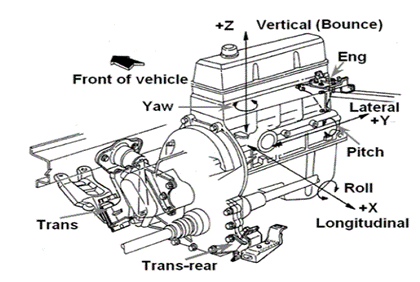
Güç Aktarma Organı Montaj Sistemi Uygulaması
- Motorun ürettiği yükleri (tork ve atalet) desteklemek ve bunlara dayanmak.
- Motorun hareketini ve açısını sınırlamak.
- Motorun öz modlarını kontrol ederek titreşim kontrolünü iyileştirmek.
- Motordan gelen titreşimleri filtreleyerek zararlı uğultuyu önlemek.
Şekil 2. Motor Modeli
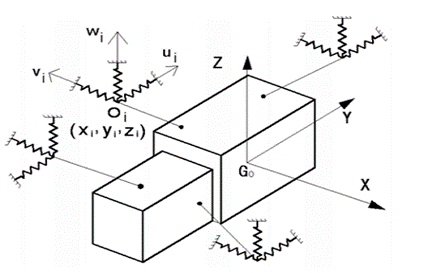
Şekil 3. Tipik Motor Montaj Sistemi
Motor Montajlarında Yorulmayı Anlamak
Yorulma, malzemede zamanla gerilme değişikliklerine neden olan döngüsel yüklemelerden kaynaklanır. Motor montajları, motor çalışmasından, yol düzensizliklerinden ve termal genleşmeden kaynaklanan dinamik yüklere maruz kalır. CI motor montajlarında yorulmayı etkileyen temel faktörler şunlardır:
- Yük Döngüleri
- Malzeme Özellikleri
Malzeme:
1-Kayma Modülü (μ): katsayısı, kauçuk malzemenin kayma davranışını tanımlar. Sıkıştırılamaz hiperelastik malzemeler için ile kayma modülü (μ) arasındaki ilişki şu şekildedir:
μ=2*
2- Hacim Modülü (K) ile : Hiperelastik malzeme modellerinde parametresi, sıkıştırılabilirliği temsil eden hacim modülü K ile ilişkilidir. İlişki şu şekildedir:
D1=2/K
NR_filled_50N330.ki
NR: Doğal Kauçuk anlamına gelir.
Filled: Malzeme dolgu malzemeleri ile takviye edilmiştir.
- NR_filled_50N330.ki
- NR: Doğal Kauçuk anlamına gelir.
- Filled: Malzeme dolgu malzemeleri ile takviye edilmiştir.
50N330:
- Dolgu malzemesinin türünü ve miktarını ifade eder.
- 50: Kauçuk bileşiğindeki dolgu malzemesinin ağırlıkça yüzdesini ifade eder.
- N330: Kauçuk endüstrisinde yaygın olarak kullanılan belirli bir siyah karbon sınıfını ifade eder. N330, aşınma direnci ile işlenebilirlik arasında bir denge sağlamasıyla bilinir.
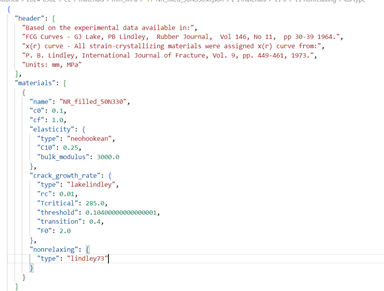
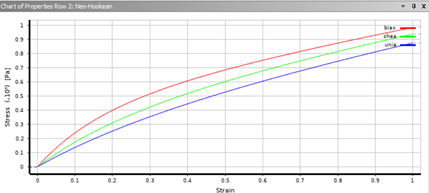
Şekil 4. Hiperelastik Model
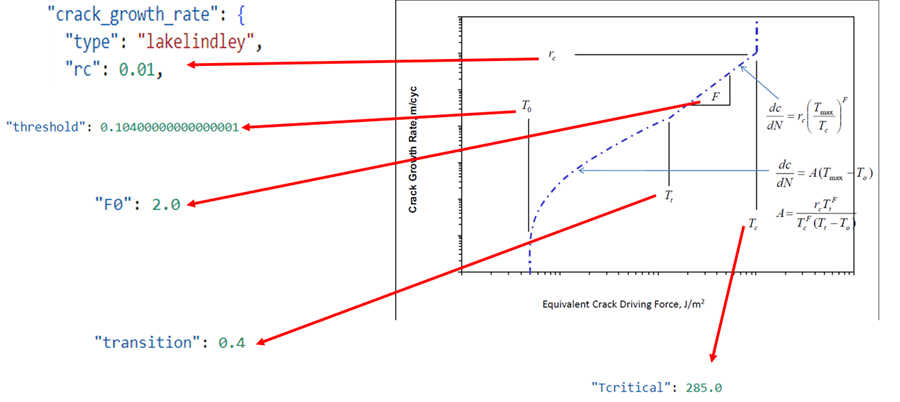
Şekil 5. Çatlak Büyüme Yasası
Tasarım Geometrisi:
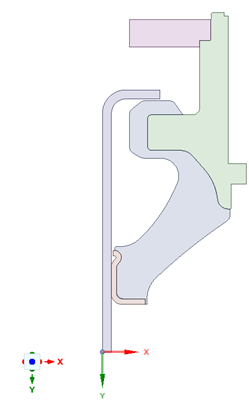
Şekil 6. Orijinal Geometri ve Basitleştirilmiş Geometri
Ön İşleme (Preprocessing):
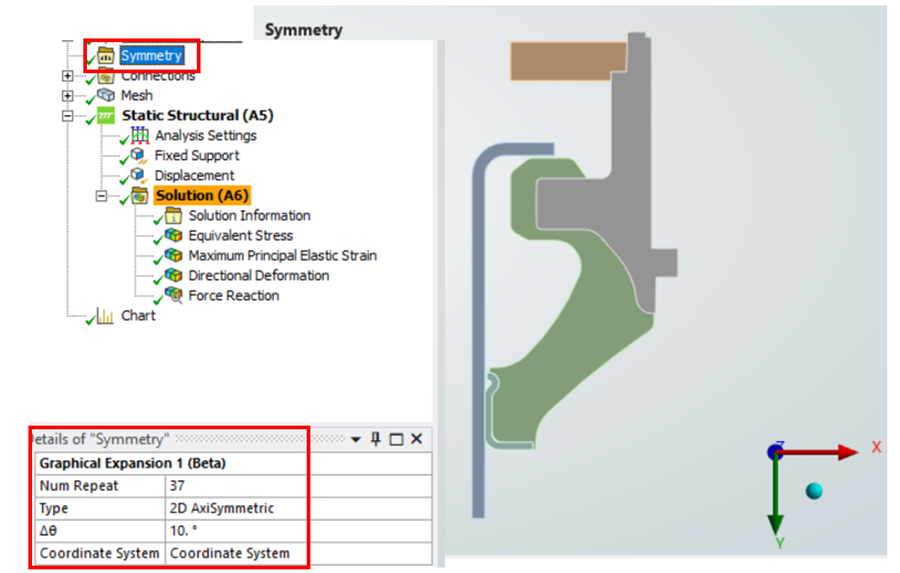
Şekil 7. Eksenel Simetri Tanımı
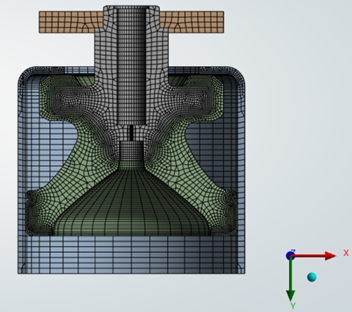
Şekil 8. Ağ (Mesh)
Sınır Şartları:
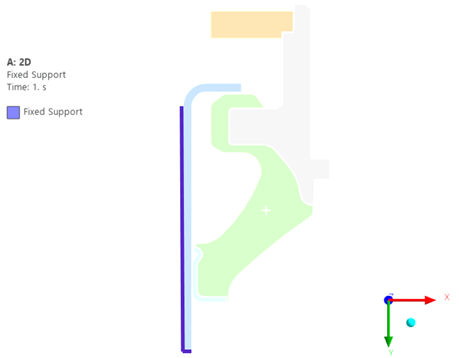
Şekil 9. Sabit Destek
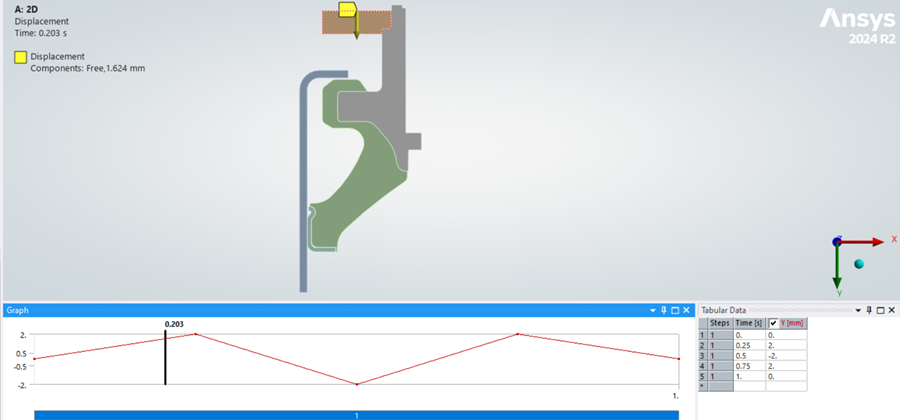
Şekil 10. Yer Değiştirme Yüklemeleri
Sonuçlar:
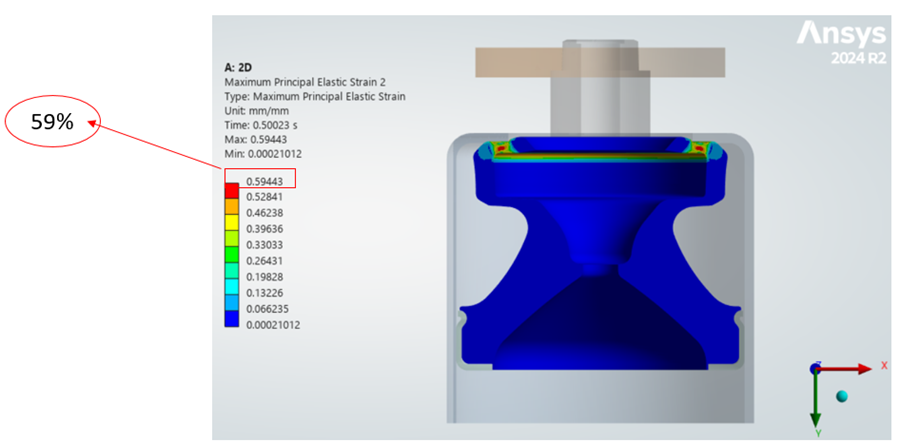
Şekil 11. Maksimum Ana Gerinim
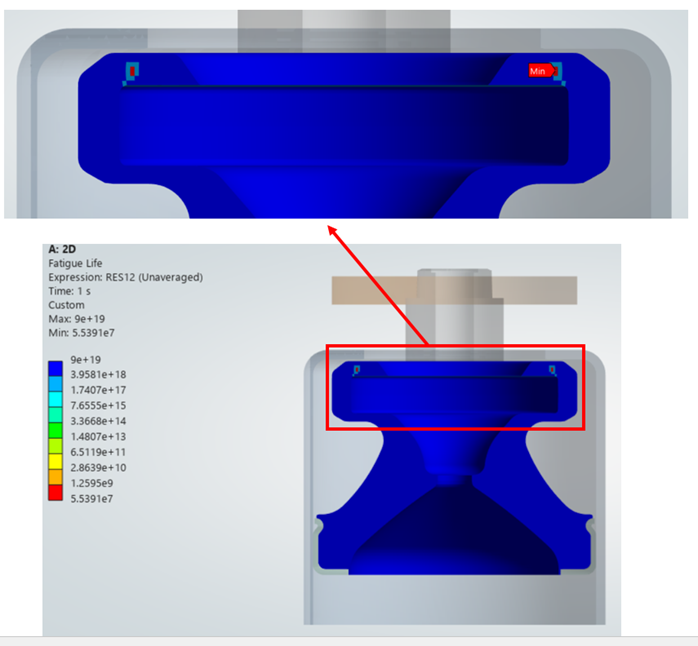
Şekil 12. Yorulma Ömrü
(Post-Processing):
CED:
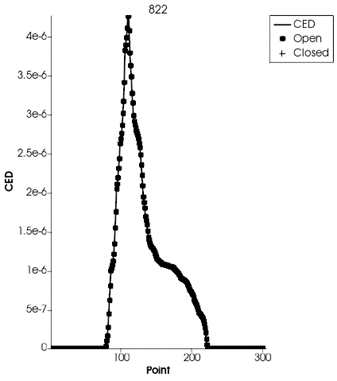
Şekil 13. CED Grafik
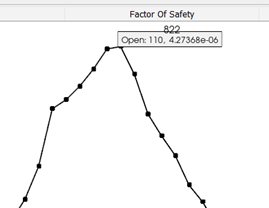
Bu durumda, semboller açık çatlakları gösteren daireleri temsil eder. Endurica, herhangi bir anda bir çatlağın açık mı yoksa kapalı mı olduğunu izler. Çekme yüklemesi altında çatlaklar açıktır, ancak burada, basma altındaki kayma nedeniyle çatlakların açık olduğunu varsayıyoruz. Maksimum çatlak enerjisi, 110. zaman noktasında kaydedilmiştir.( Toplam zaman noktası 303).
Haigh Diagram:
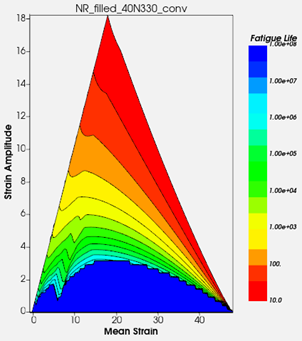
Şekil 14. Haigh Diagram
Haigh diyagramı, doğal kauçuktaki (NR) kristalleşme seviyelerini ve bunun ortalama gerinim üzerindeki etkisini göstermektedir. Kristalleşme olgusu, özellikle orta düzeyde ortalama gerinim ve düşük gerinim genlikleri bulunan bölgelerde yorulma ömrünü artırmaya katkıda bulunur. Bu etki, diyagramın daha uzun ömür bölgelerinde görüldüğü gibi parçanın dayanıklılığını artırmada kritik bir rol oynar.
Ömür:
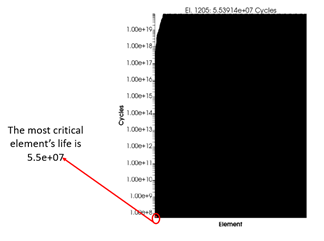
Şekil 15. Ömür Histogram
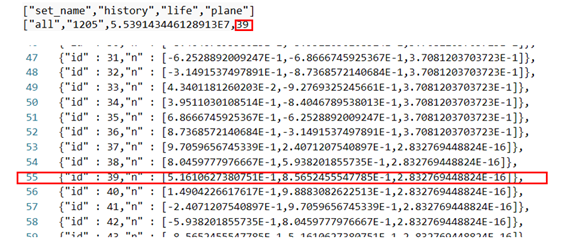
Histogram, elemanlar arasındaki yorulma ömrü dağılımını göstermektedir. En kritik eleman olan 1205, 5.5e+07 döngü ömrü sergilemektedir. Arızanın çok küçük bir bölgede yoğunlaştığı, bileşenin geri kalanının ise önemli ölçüde daha güvenli kaldığı açıkça görülmektedir. Bu durum, yorulmaya karşı lokal hassasiyeti vurgulamaktadır.
Güvenlik Faktörü:
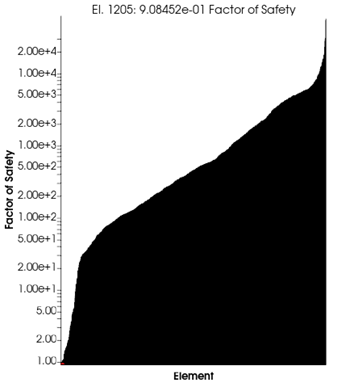
Şekil 16. Güvenlik Faktörü
Lake-Lindley modeli kullanılarak çatlak büyümesi analiz edildiğinde, eğer tüm elemanlar güvenli bir koşul gösteriyorsa, parça sonsuz ömre sahip olarak kabul edilir. Bizim durumumuzda, en kritik eleman için güvenlik faktörü 0.9 olarak hesaplanmıştır, bu da 1'e oldukça yakındır. Ancak histogramda gösterildiği gibi, genel elemanlar oldukça güvenlidir. Bu nedenle bu parça güvenli bir ömre sahip olarak sınıflandırılabilir.
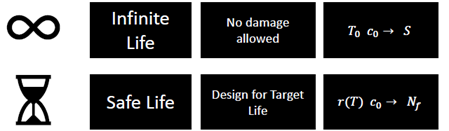
Ömür Küresi:
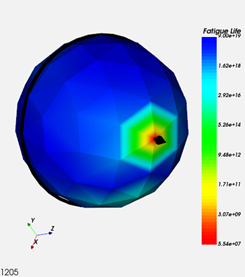
Şekil 17. Ömür Küresi
Kritik düzlem, çatlağın büyüdüğü düzlemdir. Ömür küresindeki ok, kritik düzleme dik olan normali temsil eder. Ok, tüm yönelimleri tarar ve en kısa yorulma ömrüne sahip kritik elemanlara karşılık gelen yönelimi belirler. Ayrıca, aşağıda gösterildiği gibi, çıktı dosyası kritik düzlemin koordinatlarını belirlemek için kullanılabilir.