Fatigue Analysis of CI Engine Mountings: Enhancing Durability and Performance
Fatigue Analysis of CI Engine Mountings: Enhancing Durability and Performance
Introduction
The main idea behind Endurica Solutions:
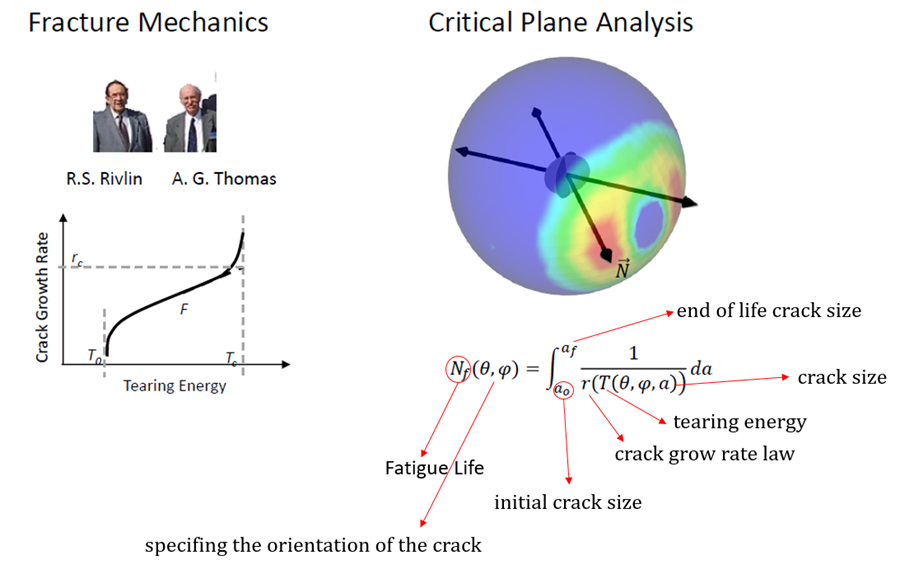
Figure 1, Crack Growth Law
Fracture mechanics is an approach to analyzing and testing rubbers, first pioneered by Rivlin and Thomas. The core idea is that the strength of a material, whether or not a crack grows and its rate of growth, can be characterized using tearing energy (energy release rate).
- On the X-axis, tearing energy reflects the severity of the load applied to the crack. As the load increases, the crack grows faster.
- The powerful concept in fracture mechanics is that if crack growth is characterized in terms of tearing energy, the shape of the crack becomes irrelevant. All the specifics combine into a single fundamental curve that links the crack growth rate to the tearing energy.
Fatigue Life Prediction
This approach offers significant advantages both experimentally and analytically. To predict fatigue life, we calculate an integral:
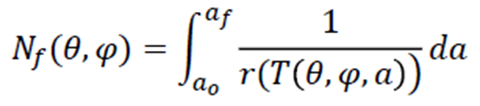
Crack Orientation and Critical Plane Analysis
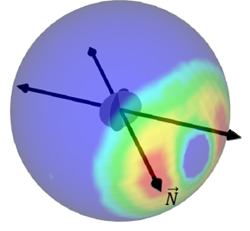
Fatigue life depends on θ and φ , which define the orientation of the crack.
- The arrows represent normal vectors that define the plane of a crack.
- Associated with each normal vector is a small, penny-shaped crack plane.
In critical plane analysis, we evaluate all possible crack orientations (vectors in all directions). For each plane, we solve the integral to calculate the fatigue life.
- When plotted as a contour plot over a spherical domain, the fatigue life distribution is visualized.
- Blue regions indicate long lives.
- Red regions indicate short lives.
The goal is to identify the crack orientation that produces the deepest red, representing the minimum life prediction. This orientation highlights the most critical plane for crack growth.
Powertrain Mounting System Application:
- Support and withstand the loads generated by the engine (torque and inertia)
- Limit the travel and angle of the engine
- Control the engine eigen modes improving shake control.
- Filter the vibrations coming from the engine damaging booming.
Understanding Fatigue in Engine Mountings
Fatigue occurs due to cyclic loading, which induces stress variations in the material over time. Engine mountings are subjected to dynamic loads resulting from engine operation, road irregularities, and thermal expansion. Key factors influencing fatigue in CI engine mountings include:
- Load Cycles.
- Material Properties:
Material:
1- Shear Modulus (μ): C10 Coefficient defines shear behaviour of rubber material For incompressible hyperelastic materials, the relationship between and the shear modulus μ is:
μ=2*
2- Bulk Modulus (K) to : The parameter is related to the bulk modulus K in hyperelastic material models and represents compressibility. The relationship is:
=
NR_filled_50N330.ki
NR: stands for Natural Rubber.
Filled: the material is reinforced with fillers.
- Fillers are typically added to enhance mechanical properties such as strength, stiffness, or wear resistance. Common fillers for rubber include carbon black or silica.
50N330:
- Refers to the type and amount of the filler.
- 50: Indicates the percentage (by weight) of the filler in the rubber compound.
- N330: Refers to a specific grade of carbon black, commonly used in the rubber industry. N330 is known for its balance between abrasion resistance and processability.
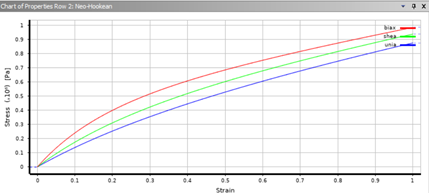
Figure 2. Hyperelastic Model
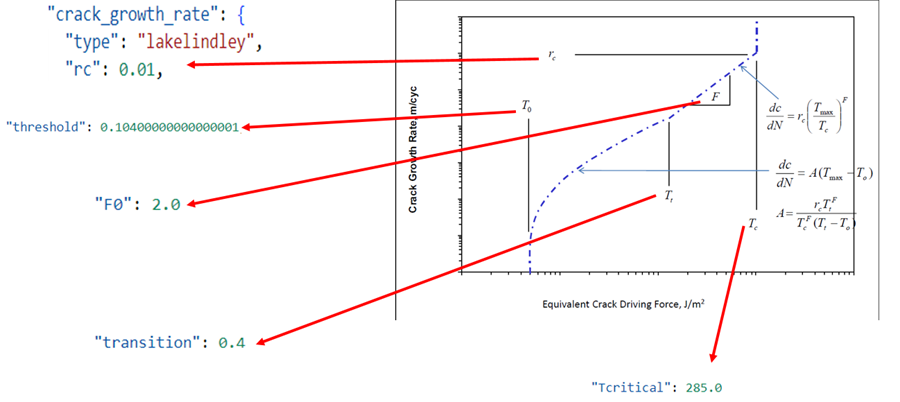
Figure 3. Crack Growth Law
Design Geometry:
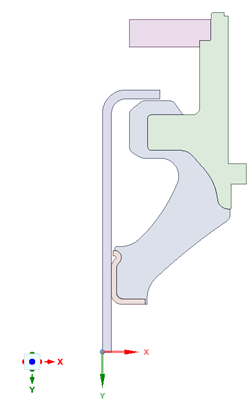
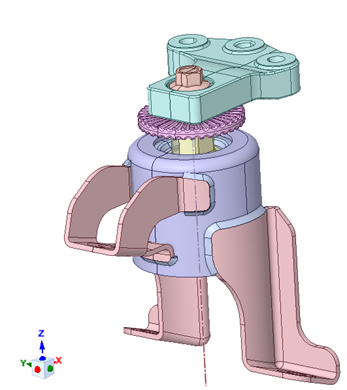
Figure 4. Original Geometry vs simplified
Preprocessing:
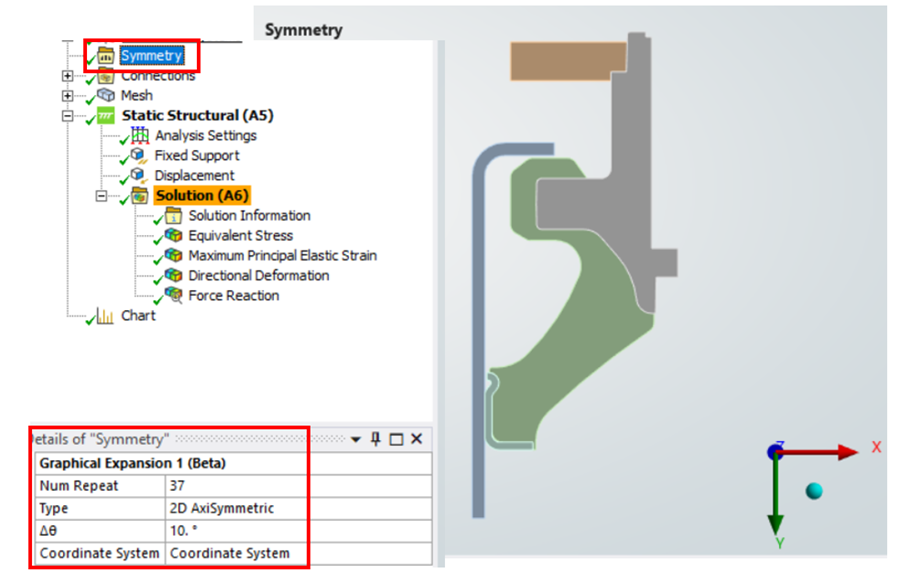
Figure 5. Axisymmteric definition
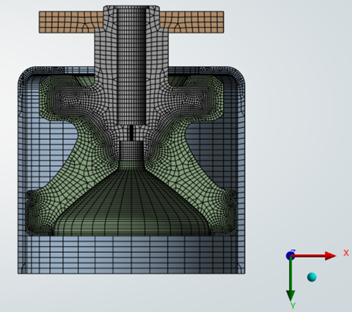
Figure 6. Mesh
Boundary Conditions:
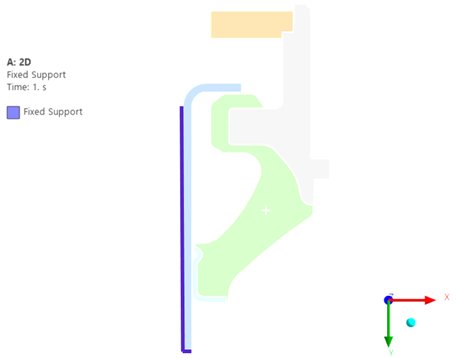
Figure 7. Fixed Suport
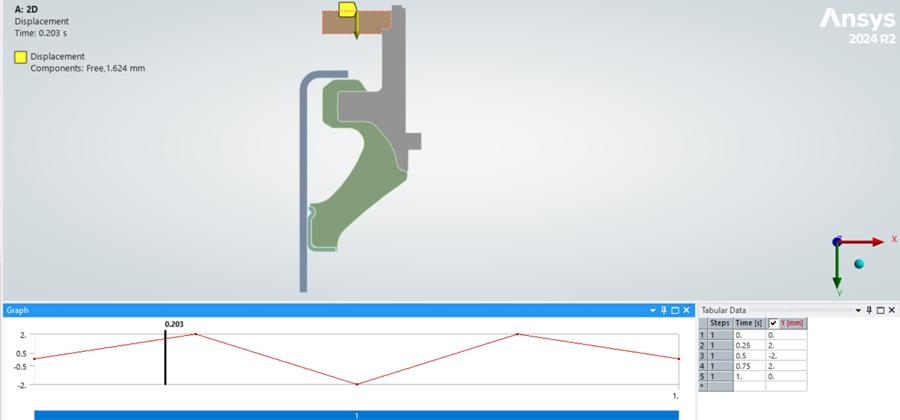
Figure 8. Displacement Loadings
Results:
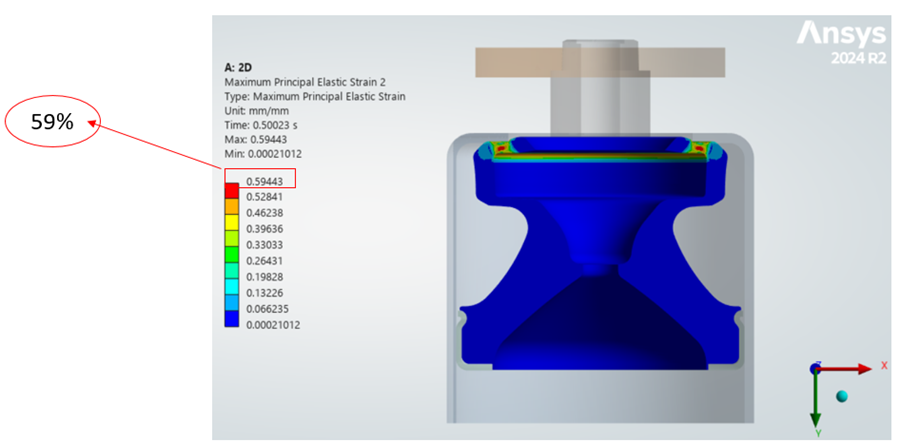
Figure 9.Maximum Principal strain
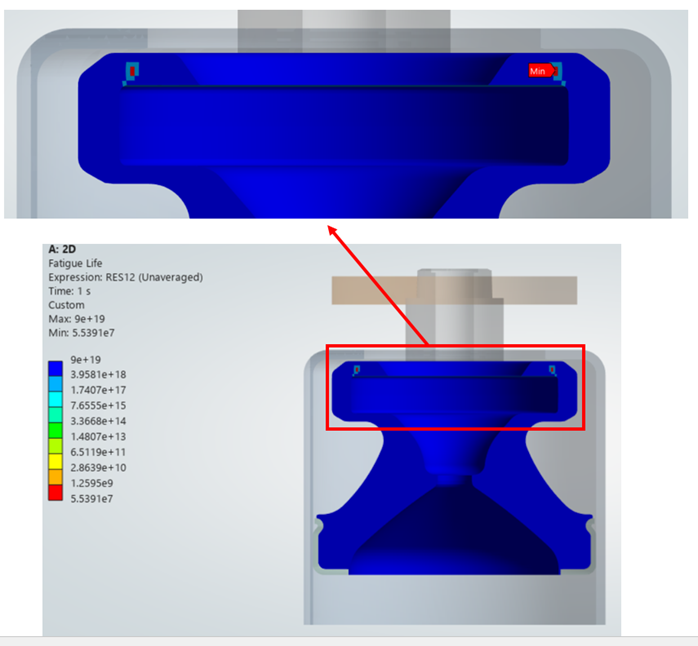
Figure 10. Fatigue Life
Post-processing:
CED:
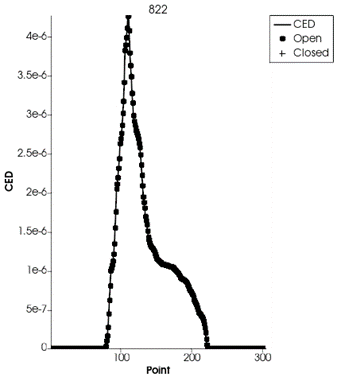
Figure 11. CED Plot
In this case, the symbols represent circles indicating open cracks. Endurica tracks whether a crack is open or closed at any given moment. Under tensile loading, cracks are open, but here we assume that cracks are open due to shear under compression. The peak cracking energy was recorded at the 110th time point.(Total time points is 303)
Haigh Diagram:
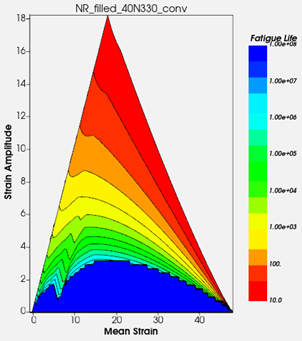
Figure 12. haigh Diagram
This Haigh diagram reveals the levels of crystallization in natural rubber (NR) and its effect on mean strain. The crystallization phenomenon contributes to enhancing fatigue life, particularly in regions with moderate mean strain and lower strain amplitudes. This effect is critical in extending the part's durability, as seen in the longer life zones of the diagram.
Life:
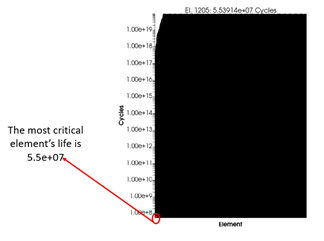
Figure 13. Life Histogram
This histogram illustrates the fatigue life distribution across the elements, with the most critical element being 1205, exhibiting a life of 5.5e+07 cycles. It is evident that failure is concentrated in a very small region, while the rest of the component remains significantly safer, highlighting localized susceptibility to fatigue.
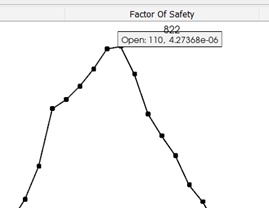
Factor of safety:
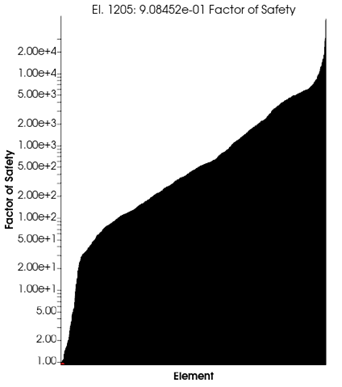
Figure 14. Factor of Safety
Using the Lake-Lindley model for crack growth, if all elements show a safe condition, the part is considered to have infinite life. In our case, the safety factor for the most critical element was calculated as 0.9, which is very close to 1. However, the overall elements are highly safe, as shown in the histogram. Therefore, this part can be classified as having a safe life.
Life Sphere:
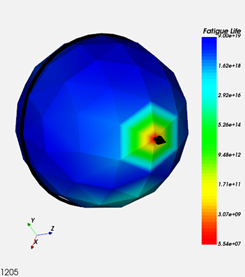
Figure 15. Life Sphere
The critical plane is the plane along which the crack grows. The arrow in the life sphere represents the normal to the critical plane. The arrow scans through all orientations and identifies the orientation corresponding to the critical elements with the shortest fatigue life. Additionally, the output file can be used to determine the coordinates of the critical plane as shown below.
Note:
- In this example, the loading conditions have been simplified and do not reflect real-world scenarios. For more accurate and realistic loading conditions, Endurica DT can be employed.
- The material properties were sourced from Endurica’s material library, which relies on data derived from published literature.
- The geometry used in this analysis was obtained from Mr. Nitin Rana’s course on Udemy.
- It is important to note that the axisymmetric approach is not suitable for non-symmetric geometries and loading conditions.